Trabajo, potencia

En mecánica, el trabajo efectuado por una fuerza aplicada sobre una partícula durante un cierto desplazamiento se define como el producto , dependiente de la trayectoria y, por lo tanto, no constituye una variable de estado. La unidad básica de trabajo en el Sistema Internacional es Newton por metro y se denomina Julio.

Fórmulas

Esquema.

En trayectorias lineales se expresa como:

siendo

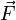•  es el vector resultante de todas las fuerzas aplicadas, que para el caso deben tener la misma dirección que el vector desplazamiento pero no necesariamente el mismo sentido. Si los vectores tienen dirección opuesta, es decir quedan como rectas secantes formando un ángulo recto el trabajo efectuado es 0.

•  es el vector desplazamiento

donde  indica la componente tangencial de la fuerza a la trayectoria.

Para calcular el trabajo a lo largo de toda la trayectoria basta con integrar entre los puntos inicial y final de la curva. En el caso más simple de una fuerza constante  aplicada sobre una distancia , el trabajo realizado se expresa como la formula siguiente:

Relación entre trabajo y energía

También se llama trabajo a la energía usada para deformar un cuerpo o, en general, alterar la energía de cualquier sistema físico. El concepto de trabajo está ligado íntimamente al concepto de energía y ambas magnitudes se miden en la misma unidad, el julio.

Esta ligazón puede verse en el hecho que, del mismo modo que existen distintas definiciones de energía para la mecánica y la termodinámica, también existen distintas definiciones de trabajo en cada rama de la física. Es una magnitud de gran importancia para establecer nexos entre las distintas ramas de la física.

Trabajo y energía son conceptos que empezaron a utilizarse cuando se abordó el estudio del movimiento de los cuerpos.

Potencia

En Física, potencia es la cantidad de trabajo efectuado por unidad de tiempo. Esto es equivalente a la velocidad de cambio de energía en un sistema o al tiempo empleado en realizar un trabajo, según queda definido por:

,

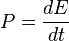donde

• P es la potencia
• E es la energía o trabajo
• t es el tiempo.

La potencia se puede considerar en función de la intensidad y la superficie:

P = I · S

• P es la potencia realizada
• I es la intensidad
• S es la superficie

La unidad de potencia en el Sistema internacional (SI) es el vatio (W), el cual es equivalente a un julio por segundo.

Fuera del SI también se utiliza el caballo de vapor (CV), equivalente a la potencia necesaria para elevar verticalmente un peso de 75 kgf a una velocidad constante de 1 m/s (movimiento uniforme). Teniendo en cuenta que un kilopondio o kilogramo-fuerza (kg-f) es la fuerza ejercida sobre una masa de 1 kg por la gravedad estándar en la superficie terrestre, esto es, 9,80665 m/s², entonces

En la vida cotidiana, interesa saber no sólo el trabajo que se pueda efectuar, sino también la rapidez con que se realiza.

Una persona está limitada en el trabajo que pueda efectuar, no sólo por la energía total necesaria, sino también por la rapidez con que transforma esa energía.

Se define potencia como la rapidez a la cual se efectúa trabajo, o bien, como la rapidez de transferencia de energía en el tiempo.

Potencia = W/t = trabajo/tiempo = energía transformada/tiempo.

En el Sistema Internacional la potencia se expresa en
Joules por segundo, unidad a la que se le da el nombre
Watt (W), 1 W = 1J/s.

Cuando decimos que una ampolleta consume 60 watts, estamos diciendo que transforma en cada segundo 60 Joules de energía eléctrica en energía luminosa o térmica.

Para potencias elevadas se usa el caballo de fuerza, abreviado hp, que equivale a 746 Watts.

1 hp = 746 watts

A veces conviene expresar la potencia en términos de la fuerza neta F aplicada a un objeto y de su velocidad.

P = W/t. P = W/t. Como W = Fuerza (F) * desplazamiento (x) = Fx, P = Fx/t.

Si la velocidad v es constante, v = x/t obteniendo,
P = Fv, esto es, fuerza por velocidad.

Si la velocidad v es variable se usa la potencia instantánea definida como
P = dW/dt donde p es el símolo de derivada.
O sea la potencia instantánea es el trabajo por unidad de tiempo durante un pequeñísimo intervalo de tiempo dt.

Como dW = Fdx y v = dx/dt resulta
P = Fv
esto es, fuerza por velocidad instantánea.

Ejemplo.
Calcule la potencia que requiere requiere un automóvil de 1.200 kg para las siguientes situaciones:

a) El automóvil sube una pendiente de 8º a una velocidad constante de 12 m/s.
b) El automóvil acelera de 14 m/s a 18 m/s en 10 s para adelantar otro vehículo, en una carretera horizontal. Suponga que la fuerza de roce o fuerza de retardo es constante e igual a Fr = 500 N.

F denota la fuerza que impulsa al auto.

SOLUCION.

a) A velocidad constante la aceleración es cero, de modo que podemos escribir:

F = Fr + mgsen
F = 500 N + 1200 kg•9,8 m/s² •sen8º = 2.137 N

Usando P = Fv, resulta P = 2.137N•12m/s = 25644 watts, que expresada en hp resulta 34,3 hp.

b) La aceleración es (18m/s - 14m/s)10s = 0,4 m/s².

Por 2ª ley de Newton, la resultante de las fuerzas externas debe ser igual a ma, masa por aceleración.

F - Fr = ma
F = 1200kg•0,4m/s² + 500N = 980 N

La potencia requerida para alcanzar los 18 m/s y adelantar es

P = Fv = 980N•18m/s = 17.640 watts ó 23,6 hp.