Teoría de la relatividad

La teoría de la relatividad incluye tanto a la teoría de la relatividad especial como a la de relatividad general, formuladas por Albert Einstein a principios del siglo XX, que pretendían resolver la incompatibilidad existente entre la mecánica newtoniana y el electromagnetismo.
La teoría de la relatividad especial, publicada en 1905, trata de la física del movimiento de los cuerpos en ausencia de fuerzas gravitatorias, en el que se hacían compatibles las ecuaciones de Maxwell del electromagnetismo con una reformulación de las leyes del movimiento.
La teoría de la relatividad general, publicada en 1915, es una teoría de la gravedad que reemplaza a la gravedad newtoniana, aunque coincide numéricamente con ella paracampos gravitatorios débiles y "pequeñas" velocidades. La teoría general se reduce a la teoría especial en ausencia de campos gravitatorios.
No fue hasta el 7 de marzo de 2010 cuando fueron mostrados públicamente los manuscritos originales de Einstein por parte de la Academia Israelí de Ciencias, aunque la teoría se había publicado en 1905. El manuscrito contiene 46 páginas de textos y fórmulas matemáticas redactadas a mano, y fue donado por Einstein a la Universidad Hebrea de Jerusalén en 1925 con motivo de su inauguración.
Conceptos principales
El supuesto básico de la teoría de la relatividad es que la localización de los sucesos físicos, tanto en el tiempo como en el espacio, son relativos al estado de movimiento del observador: así, la longitud de un objeto en movimiento o el instante en que algo sucede, a diferencia de lo que sucede en mecánica newtoniana, no son invariantes absolutos, y diferentes observadores en movimiento relativo entre sí diferirán respecto a ellos (las longitudes y los intervalos temporales, en relatividad son relativos y no absolutos).

Relatividad especial
La teoría de la relatividad especial, también llamada teoría de la relatividad restringida, fue publicada por Albert Einstein en 1905 y describe la física del movimiento en el marco de un espacio-tiempo plano. Esta teoría describe correctamente el movimiento de los cuerpos incluso a grandes velocidades y sus interacciones electromagnéticas y se usa básicamente para estudiar sistemas de referencia inerciales (no es aplicable para problemas astrofísicos donde el campo gravitatorio desempeña un papel importante).
Estos conceptos fueron presentados anteriormente por Poincaré y Lorentz, que son considerados como precursores de la teoría. Si bien la teoría resolvía un buen número de problemas del electromagnetismo y daba una explicación del experimento de Michelson-Morley, no proporciona una descripción relativista adecuada del campo gravitatorio.
Tras la publicación del artículo de Einstein, la nueva teoría de la relatividad especial fue aceptada en unos pocos años por la práctica totalidad de los físicos y los matemáticos. De hecho, Poincaré o Lorentz habían estado muy cerca de llegar al mismo resultado que Einstein. La forma geométrica definitiva de la teoría se debe a Hermann Minkowski, antiguo profesor de Einstein en la Politécnica de Zürich; acuñó el término"espacio-tiempo" (Raumzeit) y le dio la forma matemática adecuada.nota 1 El espacio-tiempo de Minkowski es una variedad tetradimensional en la que se entrelazaban de una manera insoluble las tres dimensiones espaciales y el tiempo. En este espacio-tiempo de Minkowski, el movimiento de una partícula se representa mediante su línea de universo (Weltlinie), una curva cuyos puntos vienen determinados por cuatro variables distintas: las tres dimensiones espaciales ( ,
,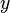 ,
, ) y el tiempo (
) y el tiempo (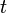 ). El nuevo esquema de Minkowski obligó a reinterpretar los conceptos de la métrica existentes hasta entonces. El concepto tridimensional depunto fue sustituido por el de suceso. La magnitud de distancia se reemplaza por la magnitud de intervalo.
). El nuevo esquema de Minkowski obligó a reinterpretar los conceptos de la métrica existentes hasta entonces. El concepto tridimensional depunto fue sustituido por el de suceso. La magnitud de distancia se reemplaza por la magnitud de intervalo.
 ,
,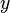 ,
, ) y el tiempo (
) y el tiempo (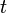 ). El nuevo esquema de Minkowski obligó a reinterpretar los conceptos de la métrica existentes hasta entonces. El concepto tridimensional depunto fue sustituido por el de suceso. La magnitud de distancia se reemplaza por la magnitud de intervalo.
). El nuevo esquema de Minkowski obligó a reinterpretar los conceptos de la métrica existentes hasta entonces. El concepto tridimensional depunto fue sustituido por el de suceso. La magnitud de distancia se reemplaza por la magnitud de intervalo.
Relatividad general
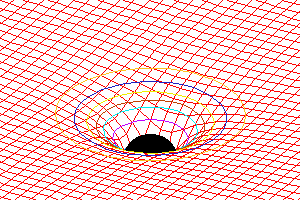
La relatividad general fue publicada por Einstein en 1915, y fue presentada como conferencia en la Academia de Ciencias Prusiana el 25 de noviembre. La teoría generaliza elprincipio de relatividad de Einstein para un observador arbitrario. Esto implica que las ecuaciones de la teoría deben tener una forma de covariancia más general que lacovariancia de Lorentz usada en la teoría de la relatividad especial. Además de esto, la teoría de la relatividad general propone que la propia geometría del espacio-tiempo se ve afectada por la presencia de materia, de lo cual resulta una teoría relativista del campo gravitatorio. De hecho la teoría de la relatividad general predice que el espacio-tiempo no será plano en presencia de materia y que la curvatura del espacio-tiempo será percibida como un campo gravitatorio.
Debe notarse que el matemático alemán David Hilbert escribió e hizo públicas las ecuaciones de la covarianza antes que Einstein. Ello resultó en no pocas acusaciones de plagio contra Einstein, pero probablemente sea más, porque es una teoría (o perspectiva) geométrica. La misma postula que la presencia de masa o energía «curva» al espacio-tiempo, y esta curvatura afecta la trayectoria de los cuerpos móviles e incluso la trayectoria de la luz.
Einstein expresó el propósito de la teoría de la relatividad general para aplicar plenamente el programa de Ernst Mach de la relativización de todos los efectos de inercia, incluso añadiendo la llamada constante cosmológica a sus ecuaciones de campo4 para este propósito. Este punto de contacto real de la influencia de Ernst Mach fue claramente identificado en 1918, cuando Einstein distingue lo que él bautizó como el principio de Mach (los efectos inerciales se derivan de la interacción de los cuerpos) del principio de la relatividad general, que se interpreta ahora como el principio de covarianza general.
Formalismo de la teoría de la relatividad
Partículas
En la teoría de la relatividad una partícula puntual queda representada por un par  , donde
, donde  es una curva diferenciable, llamada línea de universo de la partícula, y m es un escalar que representa la masa en reposo. El vector tangente a esta curva es un vector temporal llamado cuadrivelocidad, el producto de este vector por la masa en reposo de la partícula es precisamente el cuadrimomento. Este cuadrimomento es un vector de cuatro componentes, tres de estas componentes se denominan espaciales y representan el análogo relativista del momento lineal de la mecánica clásica, la otra componente denominada componente temporal representa la generalización relativista de la energía cinética. Además, dada una curva arbitraria en el espacio-tiempo, puede definirse a lo largo de ella el llamado intervalo relativista, que se obtiene a partir del tensor métrico. El intervalo relativista medido a lo largo de la trayectoria de una partícula es proporcional al intervalo de tiempo propio o intervalo de tiempo percibido por dicha partícula.
es una curva diferenciable, llamada línea de universo de la partícula, y m es un escalar que representa la masa en reposo. El vector tangente a esta curva es un vector temporal llamado cuadrivelocidad, el producto de este vector por la masa en reposo de la partícula es precisamente el cuadrimomento. Este cuadrimomento es un vector de cuatro componentes, tres de estas componentes se denominan espaciales y representan el análogo relativista del momento lineal de la mecánica clásica, la otra componente denominada componente temporal representa la generalización relativista de la energía cinética. Además, dada una curva arbitraria en el espacio-tiempo, puede definirse a lo largo de ella el llamado intervalo relativista, que se obtiene a partir del tensor métrico. El intervalo relativista medido a lo largo de la trayectoria de una partícula es proporcional al intervalo de tiempo propio o intervalo de tiempo percibido por dicha partícula.
 , donde
, donde  es una curva diferenciable, llamada línea de universo de la partícula, y m es un escalar que representa la masa en reposo. El vector tangente a esta curva es un vector temporal llamado cuadrivelocidad, el producto de este vector por la masa en reposo de la partícula es precisamente el cuadrimomento. Este cuadrimomento es un vector de cuatro componentes, tres de estas componentes se denominan espaciales y representan el análogo relativista del momento lineal de la mecánica clásica, la otra componente denominada componente temporal representa la generalización relativista de la energía cinética. Además, dada una curva arbitraria en el espacio-tiempo, puede definirse a lo largo de ella el llamado intervalo relativista, que se obtiene a partir del tensor métrico. El intervalo relativista medido a lo largo de la trayectoria de una partícula es proporcional al intervalo de tiempo propio o intervalo de tiempo percibido por dicha partícula.
es una curva diferenciable, llamada línea de universo de la partícula, y m es un escalar que representa la masa en reposo. El vector tangente a esta curva es un vector temporal llamado cuadrivelocidad, el producto de este vector por la masa en reposo de la partícula es precisamente el cuadrimomento. Este cuadrimomento es un vector de cuatro componentes, tres de estas componentes se denominan espaciales y representan el análogo relativista del momento lineal de la mecánica clásica, la otra componente denominada componente temporal representa la generalización relativista de la energía cinética. Además, dada una curva arbitraria en el espacio-tiempo, puede definirse a lo largo de ella el llamado intervalo relativista, que se obtiene a partir del tensor métrico. El intervalo relativista medido a lo largo de la trayectoria de una partícula es proporcional al intervalo de tiempo propio o intervalo de tiempo percibido por dicha partícula.
Campos
Cuando se consideran campos o distribuciones continuas de masa se necesita algún tipo de generalización para la noción de partícula. Un campo físico posee momentum y energía distribuidos en el espacio-tiempo, el concepto de cuadrimomento se generaliza mediante el llamado tensor de energía-impulso que representa la distribución en el espacio-tiempo tanto de energía como de momento lineal. A su vez un campo dependiendo de su naturaleza puede representarse por un escalar, un vector o un tensor. Por ejemplo el campo electromagnético se representa por un tensor de segundo orden totalmente antisimétrico o 2-forma. Si se conoce la variación de un campo o una distribución de materia, en el espacio y en el tiempo entonces existen procedimientos para construir su tensor de energía-impulso.
Magnitudes físicas
En relatividad, estas magnitudes físicas son representadas por vectores 4-dimensionales o bien por objetos matemáticos llamados tensores, que generalizan los vectores, definidos sobre un espacio de cuatro dimensiones. Matemáticamente estos 4-vectores y 4-tensores son elementos definidos del espacio vectorial tangente al espacio-tiempo (y los tensores se definen y se construyen a partir del fibrado tangente o cotangente de la variedad que representa el espacio-tiempo).
Igualmente además de cuadrivectores, se definen cuadritensores (tensores ordinarios definidos sobre el fibrado tangente del espacio-tiempo concebido como variedad lorentziana). La curvatura del espacio-tiempo se representa por un 4-tensor (tensor de cuarto orden), mientras que la energía y el momento de un medio continuo o el campo electromagnético se representan mediante 2-tensores (simétrico el tensor energía-impulso, antisimétrico el de campo electromagnético). Los cuadrivectores son de hecho 1-tensores, en esta terminología. En este contexto se dice que una magnitud es un invariante relativista si tiene el mismo valor para todos los observadores, obviamente todos los invariantes relativistas son escalares (0-tensores), frecuentemente formados por la contracción de magnitudes tensoriales.
El intervalo, la distancia tetradimensional, se representa mediante la expresión 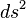 , que se calcula del siguiente modo:
, que se calcula del siguiente modo:
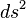 , que se calcula del siguiente modo:
, que se calcula del siguiente modo:
Los intervalos pueden ser clasificados en tres categorías: Intervalos espaciales (cuando  es negativo), temporales (si
es negativo), temporales (si  es positivo) y nulos (cuando
es positivo) y nulos (cuando  ). Como el lector habrá podido comprobar, los intervalos nulos son aquellos que corresponden a partículas que se mueven a la velocidad de la luz, como los fotones: La distancia
). Como el lector habrá podido comprobar, los intervalos nulos son aquellos que corresponden a partículas que se mueven a la velocidad de la luz, como los fotones: La distancia 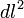 recorrida por el fotón es igual a su velocidad (c) multiplicada por el tiempo
recorrida por el fotón es igual a su velocidad (c) multiplicada por el tiempo  y por lo tanto el intervalo
y por lo tanto el intervalo  se hace nulo.
se hace nulo.
 es negativo), temporales (si
es negativo), temporales (si  es positivo) y nulos (cuando
es positivo) y nulos (cuando  ). Como el lector habrá podido comprobar, los intervalos nulos son aquellos que corresponden a partículas que se mueven a la velocidad de la luz, como los fotones: La distancia
). Como el lector habrá podido comprobar, los intervalos nulos son aquellos que corresponden a partículas que se mueven a la velocidad de la luz, como los fotones: La distancia 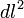 recorrida por el fotón es igual a su velocidad (c) multiplicada por el tiempo
recorrida por el fotón es igual a su velocidad (c) multiplicada por el tiempo  y por lo tanto el intervalo
y por lo tanto el intervalo  se hace nulo.
se hace nulo.
Los intervalos nulos pueden ser representados en forma de cono de luz, popularizados por el celebérrimo libro de Stephen Hawking, Historia del Tiempo. Sea un observador situado en el origen, el futuro absoluto (los sucesos que serán percibidos por el individuo) se despliega en la parte superior del eje de ordenadas, el pasado absoluto (los sucesos que ya han sido percibidos por el individuo) en la parte inferior, y el presente percibido por el observador en el punto 0. Los sucesos que están fuera del cono de luz no nos afectan, y por lo tanto se dice de ellos que están situados en zonas del espacio-tiempo que no tienen relación de causalidad con la nuestra.
Imaginemos, por un momento, que en la galaxia Andrómeda, situada a 2,5 millones de años luz de nosotros, sucedió un cataclismo cósmico hace 100.000 años. Dado que, primero: la luz de Andrómeda tarda 2 millones de años en llegar hasta nosotros y segundo: nada puede viajar a una velocidad superior a la de los fotones, es evidente, que no tenemos manera de enterarnos de lo que sucedió en dicha Galaxia hace tan sólo 100.000 años. Se dice por lo tanto que el intervalo existente entre dicha hipotética catástrofe cósmica y nosotros, observadores del presente, es un intervalo espacial ( ), y por lo tanto, no puede afectar a los individuos que en el presente viven en la Tierra: Es decir, no existe relación de causalidad entre ese evento y nosotros.
), y por lo tanto, no puede afectar a los individuos que en el presente viven en la Tierra: Es decir, no existe relación de causalidad entre ese evento y nosotros.
- Análisis
El único problema con esta hipótesis, es que al entrar en un agujero negro, se anula el espacio tiempo, y como ya sabemos, algo que contenga algún volumen o masa, debe tener como mínimo un espacio donde ubicarse, el tiempo en ese caso, no tiene mayor importancia, pero el espacio juega un rol muy importante en la ubicación de volúmenes, por lo que esto resulta muy improbable, pero no imposible para la tecnología.
Podemos escoger otro episodio histórico todavía más ilustrativo: El de la estrella de Belén, tal y como fue interpretada por Johannes Kepler. Este astrónomo alemán consideraba que dicha estrella se identificaba con una supernova que tuvo lugar el año 5 a. C., cuya luz fue observada por los astrónomos chinos contemporáneos, y que vino precedida en los años anteriores por varias conjunciones planetarias en la constelación de Piscis. Esa supernova probablemente estalló hace miles de años atrás, pero su luz no llegó a la tierra hasta el año 5 a. C. De ahí que el intervalo existente entre dicho evento y las observaciones de los astrónomos egipcios y megalíticos (que tuvieron lugar varios siglos antes de Cristo) sea un intervalo espacial, pues la radiación de la supernova nunca pudo llegarles. Por el contrario, la explosión de la supernova por un lado, y las observaciones realizadas por los tres magos en Babilonia y por los astrónomos chinos en el año 5 a. C. por el otro, están unidas entre sí por un intervalo temporal, ya que la luz sí pudo alcanzar a dichos observadores.
El tiempo propio y el intervalo se relacionan mediante la siguiente equivalencia:  , es decir, el intervalo es igual al tiempo local multiplicado por la velocidad de la luz. Una de las características tanto del tiempo local como del intervalo es su invarianza ante las transformaciones de coordenadas. Sea cual sea nuestro punto de referencia, sea cual sea nuestra velocidad, el intervalo entre un determinado evento y nosotros permanece invariante.
, es decir, el intervalo es igual al tiempo local multiplicado por la velocidad de la luz. Una de las características tanto del tiempo local como del intervalo es su invarianza ante las transformaciones de coordenadas. Sea cual sea nuestro punto de referencia, sea cual sea nuestra velocidad, el intervalo entre un determinado evento y nosotros permanece invariante.
 , es decir, el intervalo es igual al tiempo local multiplicado por la velocidad de la luz. Una de las características tanto del tiempo local como del intervalo es su invarianza ante las transformaciones de coordenadas. Sea cual sea nuestro punto de referencia, sea cual sea nuestra velocidad, el intervalo entre un determinado evento y nosotros permanece invariante.
, es decir, el intervalo es igual al tiempo local multiplicado por la velocidad de la luz. Una de las características tanto del tiempo local como del intervalo es su invarianza ante las transformaciones de coordenadas. Sea cual sea nuestro punto de referencia, sea cual sea nuestra velocidad, el intervalo entre un determinado evento y nosotros permanece invariante.
Esta invarianza se expresa a través de la llamada geometría hiperbólica: La ecuación del intervalo  tiene la estructura de una hipérbola sobre cuatro dimensiones, cuyo término independiente coincide con el valor del cuadrado del intervalo (
tiene la estructura de una hipérbola sobre cuatro dimensiones, cuyo término independiente coincide con el valor del cuadrado del intervalo ( ), que como se acaba de decir en el párrafo anterior, es constante. Las asíntotas de la hipérbola vendrían a coincidir con el cono de luz.
), que como se acaba de decir en el párrafo anterior, es constante. Las asíntotas de la hipérbola vendrían a coincidir con el cono de luz.
 tiene la estructura de una hipérbola sobre cuatro dimensiones, cuyo término independiente coincide con el valor del cuadrado del intervalo (
tiene la estructura de una hipérbola sobre cuatro dimensiones, cuyo término independiente coincide con el valor del cuadrado del intervalo ( ), que como se acaba de decir en el párrafo anterior, es constante. Las asíntotas de la hipérbola vendrían a coincidir con el cono de luz.
), que como se acaba de decir en el párrafo anterior, es constante. Las asíntotas de la hipérbola vendrían a coincidir con el cono de luz.
Imagen de la galaxia Andrómeda, tomada por el telescopio Spitzer,
tal como era hace 2,5 millones de años (por estar situada a 2,5 millones de años luz).
Teoría de la relatividad general
La teoría de la relatividad general se refiere al caso de movimientos que se producen con velocidad variable y tiene como postulado fundamental el principio de equivalencia, según el cual los efectos producidos por un campo gravitacional equivalen a los producidos por el movimiento acelerado.
La revolucionaria hipótesis formulada por Einstein fue provocada por el hecho de que la teoría de la relatividad especial, basada en el principio de la constancia de la velocidad de la luz sea cual sea el movimiento del sistema de referencia en el que se mide (tal y como se demostró en el experimento de Michelson y Morley), no concuerda con la teoría de la gravitación newtoniana: si la fuerza con que dos cuerpos se atraen depende de la distancia entre ellos, al moverse uno tendría que cambiar al instante la fuerza sentida por el otro, es decir, la interacción tendría una velocidad de propagación infinita, violando la teoría especial de la relatividad, que señala que nada puede superar la velocidad de la luz.
Tras varios intentos fallidos de acomodar la interacción gravitatoria con la relatividad, Einstein sugirió que la gravedad no es una fuerza como las otras, sino que es una consecuencia de que el espacio-tiempo se encuentra deformado por la presencia de masa (o energía, que es lo mismo). Entonces, cuerpos como la tierra no se mueven en órbitas cerradas porque haya una fuerza llamada gravedad, sino que se mueven en lo más parecido a una línea recta, pero en un espacio-tiempo que se encuentra deformado por la presencia del Sol.

Einstein en su estudio (c. 1925)
Los cálculos de la relatividad general se realizan en un espacio-tiempo de cuatro dimensiones, tres espaciales y una temporal, adoptado ya en la teoría de la relatividad restringida al tener que abandonar el concepto de simultaneidad. Sin embargo, a diferencia del espacio de Minkowski y debido al campo gravitatorio, este universo no es euclidiano. Así, la distancia que separa dos puntos contiguos del espacio-tiempo en este universo es más complejo que en el espacio de Minkowski.
Con esta teoría se obtienen órbitas planetarias muy similares a las que se obtienen con la mecánica de Newton. Uno de los puntos de discrepancia entre ambas, la anormalmente alargada órbita del planeta Mercurio, que presenta un efecto de rotación del eje mayor de la elipse (aproximadamente un grado cada diez mil años), había sido observado experimentalmente algunos años antes de enunciarse la teoría de la relatividad, y no podía ser explicado con las leyes de Newton. La órbita descrita, sin embargo, cumplía las predicciones relativistas, sirviendo así de confirmación experimental de la teoría de Einstein.
Un efecto que corroboró tempranamente la teoría de la relatividad general es la deflexión que sufren los rayos de luz en presencia de campos gravitatorios. Los rayos luminosos, al pasar de una región de un campo gravitatorio a otra, deberían sufrir un desplazamiento en su longitud de onda (el desplazamiento gravitacional al rojo o desplazamiento de Einstein), lo que fue comprobado midiendo el desplazamiento aparente de una estrella, con respecto a un grupo de estrellas tomadas como referencia, cuando los rayos luminosos provenientes de ella rozaban el Sol.
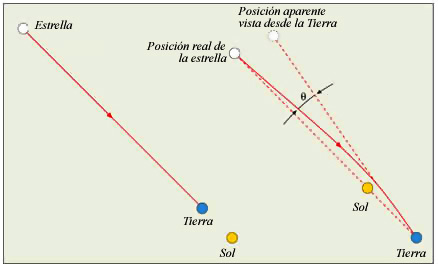
Desplazamiento de Einstein
Para evitar el deslumbramiento del observador por los rayos solares, la verificación se llevó a cabo aprovechando un eclipse total de Sol que tuvo lugar en 1919. La estrella fue fotografiada dos veces, una en ausencia y otra en presencia del eclipse. Así, midiendo el desplazamiento aparente de la estrella respecto a las estrellas de referencia, se obtenía el ángulo de desviación que resultó ser muy cercano al que Einstein había previsto.
El concepto de tiempo resultó profundamente afectado por la relatividad general. Un sorprendente resultado de esta teoría es que el tiempo debe transcurrir más lentamente cuanto más fuerte sea el campo gravitatorio en el que se mida. Esta predicción también fue confirmada por la experiencia en 1962. De hecho, muchos de los modernos sistemas de navegación por satélite tienen en cuenta este efecto, ya que de otro modo darían errores en el cálculo de la posición de varios kilómetros.
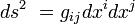

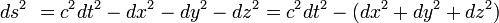

No hay comentarios:
Publicar un comentario